فرمول خاصی برای محاسبه دمای طرف دیگر پتو نسوز سرامیکی در هنگام اعمال حرارت وجود ندارد. توزیع دمای پتوی نسوز به عوامل مختلفی مانند خواص مواد تشکیل دهنده پتو، شار حرارتی اعمال شده و شرایط مرزی بستگی دارد.
فهرست مطلب
Toggleبا این حال، اگر شرایط حالت پایدار را فرض کنیم، یک روش ممکن برای محاسبه، استفاده از قانون هدایت حرارتی فوریه برای تخمین دما در طرف دیگر است. این قانون بیان می کند که شار حرارتی Q (نرخ انتقال حرارت در واحد سطح) از طریق یک ماده متناسب با گرادیان دما در سراسر ماده است.
از نظر ریاضی، این را می توان به صورت زیر بیان کرد:

فرمول محاسبه دمای طرف دیگر پتو نسوز سرامیکی
Q = k * A * (T2 – T1) / L
Q is the heat flux (W),
Q شار حرارتی (W) است،
k is the thermal conductivity of the blanket material (W/m·K),
k هدایت حرارتی پتو (W/m·K) است.
A is the cross-sectional area of the blanket perpendicular to the heat flow (m²),
A سطح مقطع پتو عمود بر جریان گرما (m²) است.
T2 is the temperature on the other side of the blanket (K or °C),
T2 دمای طرف دیگر پتو (K یا درجه سانتیگراد) است.
T1 is the temperature on the side where heat is applied (K or °C),
T1 دمای سمتی است که گرما اعمال می شود (K یا درجه سانتیگراد) ،
L is the thickness of the blanket (m).
L ضخامت پتو (m) است.
با تنظیم مجدد معادله، می توانیم برای T2 حل کنیم:
T2 = (Q * L) / (k * A) + T1
نمونه مثالی برای فرمول محاسبه دمای طرف دیگر پتو نسوز سرامیکی
فرض کنید یک پتو نسوز سرامیکی با ضخامت 10 سانتی متر (1/0متر) و هدایت حرارتی (k) 1 W/mK داریم. دمای یک طرف پتو 100 درجه سانتیگراد (373 کلوین) است و ما می خواهیم دمای طرف دیگر را تخمین بزنیم.
q = (k * A * (T2 – T1)) / d
q = (1 * 1 * (T2 – 373)) / 0.1
حال، فرض کنید میخواهیم دمای طرف دیگر پتو را زمانی که شار حرارتی 50 وات است تخمین بزنیم. با تنظیم مجدد فرمول، می توانیم برای T2 حل کنیم
Q50 = (1 * 1 * (T2 – 373)) / 0.1
T2 = 5 + 373 = 378 K

چگونه می توان قانون هدایت حرارتی فوریه را برای هدایت حرارتی پتوهای نسوز سرامیکی دقیق تر کرد؟
برای اینکه قانون هدایت حرارتی فوریه برای رسانایی حرارتی پتوهای نسوز سرامیکی دقیق تر شود، باید چندین عامل مهم را در نظر گرفت:
- ناهمسانگردی: پتوهای نسوز سرامیکی اغلب رسانایی حرارتی ناهمسانگرد از خود نشان می دهند، به این معنی که رسانایی حرارتی ممکن است در جهات مختلف متفاوت باشد. بنابراین، ترکیب این ناهمسانگردی در مدل هدایت حرارتی، با در نظر گرفتن جهت یا تراز الیاف های سرامیکی پتو ضروری است.
- تخلخل: پتوهای نسوز سرامیکی به طور کلی ساختار متخلخل دارند که بر هدایت حرارتی آنها تأثیر می گذارند. اندازه، شکل و توزیع منافذ می تواند به طور قابل توجهی بر انتقال حرارت تأثیر بگذارند. یک مدل دقیق تر باید تاثیر تخلخل را بر هدایت حرارتی موثر پتو را در برگیرد.
- فعل و انفعال فیبرها: پتوهای نسوز سرامیکی از الیاف به هم پیوسته تشکیل شده اند که می توانند بر انتقال حرارت تأثیر بگذارند. تعامل بین الیاف، مانند مقاومت تماس یا پل حرارتی، باید در نظر گرفته شود تا عملکرد حرارتی واقعی پتو را با دقت بیشتری منعکس کند.
- وابستگی به دما: هدایت حرارتی مواد سرامیکی، از جمله پتوهای نسوز، اغلب با دما تغییر می کند. در نظر گرفتن وابستگی دما در مدل هدایت حرارتی، با استفاده از معادلات مناسب یا دادههای تجربی برای ثبت این تغییرات مهم است.
- اثر ضخامت: ضخامت پتو نسوز می تواند بر انتقال حرارت تأثیر بگذارد. گنجاندن اثر ضخامت با در نظر گرفتن هدایت گرما در امتداد جهت ضخامت می تواند دقت مدل هدایت حرارتی را بهبود بخشد.
- اعتبار سنجی آزمایشی: دقیق ترین راه برای تعیین رسانایی حرارتی پتوهای نسوز سرامیکی از طریق اندازه گیری های تجربی است. انجام آزمایشهای هدایت حرارتی تحت شرایط مربوطه و مقایسه نتایج با پیشبینیهای مدل به اعتبارسنجی و اصلاح دقت مدل کمک میکند.
برای بهبود دقت، ممکن است یک مدل هدایت حرارتی پیچیدهتر ایجاد شود که این عوامل را در خود جای دهد و بتوان آن را به دادههای تجربی برازش داد. این میتواند شامل عبارات اضافی یا معادلات اصلاح شده در مقایسه با قانون فوریه باشد که ناهمسانگردی، تخلخل، برهمکنش الیاف، وابستگی به دما و اثر ضخامت را در نظر میگیرد.
چگونه می توان اثر تخلخل را بر قانون هدایت حرارتی فوریه پتوهای نسوز سرامیکی اعمال کرد؟
برای اعمال اثر تخلخل بر قانون هدایت حرارتی فوریه برای پتوهای نسوز سرامیکی، می توانید از مراحل زیر استفاده کنید:
- درک مفهوم تخلخل: تخلخل به وجود فضاهای خالی یا منافذ در یک ماده اشاره دارد. در زمینه هدایت حرارتی، تخلخل بر توانایی یک ماده برای هدایت گرما تأثیر می گذارد.
- همبستگی نظری یا تجربی را بدست آورید: به دنبال معادلات نظری یا همبستگی های تجربی باشید که تخلخل ماده را به رسانایی حرارتی آن مرتبط می کند. این همبستگی ها اغلب به صورت تجربی یا از طریق مدل های نظری به دست می آیند.
- اندازه گیری یا تخمین تخلخل: اندازه گیری یا تخمین تخلخل پتو نسوز سرامیکی، این را می توان با استفاده از تکنیکهای مختلفی مانند تجزیه و تحلیل تصویر، تخلخل سنجی نفوذ جیوه یا اندازه گیری چگالی انجام داد.
- تعیین رسانایی حرارتی: از قانون هدایت حرارتی فوریه برای محاسبه رسانایی حرارتی پتو نسوز سرامیکی بدون در نظر گرفتن تخلخل استفاده کنید. این را می توان با اندازه گیری گرادیان دما در سراسر ماده و اعمال معادله انجام داد:
q = -k * ∇T,
که در آن q شار گرما، k هدایت حرارتی، و ∇T گرادیان دما است.
- اعمال اثر تخلخل: از همبستگی نظری یا تجربی به دست آمده در مرحله 2 برای اصلاح مقدار هدایت حرارتی بر اساس تخلخل استفاده کنید. این ممکن است شامل ضرب رسانایی حرارتی در یک ضریب تصحیح تخلخل یا استفاده از یک معادله خاص ارائه شده توسط معادلات همبستگی باشد.
- محاسبه هدایت حرارتی موثر: هدایت حرارتی اصلاح شده به دست آمده در مرحله 5 را در ضریب تخلخل ضرب کنید تا رسانایی گرمایی موثر پتوی نسوز سرامیکی را با اثر تخلخل به دست آورید.
- اعتبارسنجی نتایج: رسانایی گرمایی موثر محاسبه شده را با داده های تجربی برای اعتبار سنجی مقایسه کنید.
توجه داشته باشید که معادلات و همبستگی های خاص مورد استفاده ممکن است بسته به محدوده مواد و تخلخل در نظر گرفته شده متفاوت باشد. توصیه میشود برای ارتباطهای خاص مربوط به پتوهای نسوز سرامیکی، به مقالات تحقیقاتی مرتبط، کتابهای درسی یا پایگاههای اطلاعاتی مواد مراجعه کنید.

فرمول اصلاح شده فوریه با در نظر گرفتن تخلخل در پتو نسوز سرامیکی
برای محاسبه دمای سمت سرد یک پتوی نسوز سرامیکی با استفاده از فرمول اصلاح شده فوریه با تخلخل، باید معادله زیر را در نظر بگیرید:
𝑸 = −𝑘 × 𝐴 × 𝑑𝑇/𝑑𝑥
Where:
𝑸 is the heat flow rate (Watt),
𝑘 is the thermal conductivity of the refractory blanket (Watt/meter-Kelvin),
𝐴 is the cross-sectional area of the blanket (meter²),
𝑑𝑇/𝑑𝑥 is the temperature gradient across the refractory blanket (Kelvin/meter).
برای ترکیب تخلخل، باید معادله را با وارد کردن ضریب تخلخل (p) اصلاح کنید. معادله اصلاح شده به صورت زیر خواهد بود:
𝑸 = −𝑘 × (1 − p) × 𝐴 × 𝑑𝑇/𝑑𝑥
عبارت p-1 تخلخل پتو نسوز سرامیکی را به حساب می آورد. مطمئن شوید که مقادیر مناسب را برای 𝑘، 𝐴، dT/dx و p جایگزین کنید تا دمای سمت سرد را بدست آورید.
دو مثال عددی برای محاسبه دما سمت سرد پتو نسوز سرامیکی با فرمول اصلاح شده فوریه که در آن تخلخل در نظر گرفته شده است:
مثال 1: برای محاسبه دمای سمت سرد یک پتوی نسوز سرامیکی با در نظر گرفتن تخلخل، میتوان از فرمول فوریه اصلاحشده استفاده کرد که به عنوان معادله هدایت حرارتی مؤثر نیز شناخته میشود:
Q = (keff * A * (Thot – Tcold)) / L
Where:
Q = Heat transfer rate
keff = Effective thermal conductivity
A = Cross-sectional area
Thot = Temperature of the hot side
Tcold = Temperature of the cold side
L = Thickness of the refractory blanket
حال، با ترکیب ضریب تخلخل (P) در معادله هدایت حرارتی مؤثر، فرمول به صورت زیر در میآید:
Q = (k * (1 – P) * A * (Thot – Tcold)) / L
بیایید مثال عددی زیر را در نظر بگیریم:
k = 2.5 W/m·K (thermal conductivity of the ceramic refractory blanket)
P = 0.3 (porosity factor)
A = 1 m^2
Thot = 500°C
Tcold =?
L = 0.1 m (thickness of the refractory blanket)
Q = (k * (1 – P) * A * (Thot – Tcold)) / L
Q = 100 W (heat transfer rate)
Tcold = Thot – ((Q * L) / (k * (1 – P) * A))
Tcold = 500 – ((100 * 0.1) / (2.5 * (1 – 0.3) * 1))
Tcold ≈ 329.41°C
بنابراین دمای سمت سرد پتو نسوز سرامیکی با در نظر گرفتن تخلخل تقریباً 41/329 درجه سانتی گراد است.
مثال 2 (مثال تکمیلی): تخلخل با تأثیر بر رسانایی حرارتی ماده بر قانون فوریه تأثیر می گذارد. در مواد متخلخل، رسانایی حرارتی عموماً با افزایش تخلخل کاهش می یابد. این به این دلیل است که هوای محبوس شده در منافذ به عنوان یک عایق عمل می کند و انتقال حرارت کلی را کاهش می دهد. از نظر ریاضی، این را می توان با تبدیل رسانایی حرارتی k تابعی از تخلخل P نشان داد. بنابراین، قانون فوریه به صورت زیر می شود:
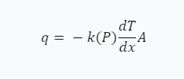
Where:
q is the heat transfer rate,
k(P) is the thermal conductivity of the material as a function of porosity P,
dT/dx is the temperature gradient in the direction of the flow,
A is the area through which heat is being transferred.
این معادله نشان میدهد که برای یک گرادیان دما و مساحت معین، مادهای با تخلخل بالاتر (و در نتیجه هدایت حرارتی پایینتر) نرخ انتقال حرارت کمتری داریم. با این حال، مهم است که توجه داشته باشید که این یک ساده سازی است. شرایط دنیای واقعی می تواند بسیار پیچیده تر باشد و ممکن است به مدل ها یا شبیه سازی های پیچیده تری برای پیش بینی دقیق نیاز داشته باشد. اگر نیاز به انجام این محاسبات برای یک برنامه خاص دارید، توصیه میکنیم با یک متخصص مشورت کنید یا از نرم افزار تخصصی طراحی شده برای این منظور استفاده کنید.
** فرض کنید کوره ای با دمای صفحه داغ T_hot = 1500 کلوین داریم. کوره با یک پوشش نسوز سرامیکی با ضخامت d = 0.1 متر (10 سانتی متر) و هدایت حرارتی k = 0.1 W/(m*K) پوشیده شده است.
طبق قانون فوریه، نرخ انتقال حرارت q از طریق پتو را می توان به صورت زیر محاسبه کرد:
dT/dx گرادیان دما است که می تواند به صورت (T_hot – T_cold) / dx محاسبه شود و A ناحیه ای است که گرما از طریق آن منتقل می شود.
اگر شار انتقال حرارت q و مساحت A را بدانیم، میتوانیم این معادله را برای حل دمای قسمت سرد T_cold دوباره مرتب کنیم:
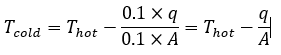
پس هنگام استفاده از پتوهای نسوز سرامیکی ما فقط نیاز به محاسبه سطح مقطع مورد نیاز در کار خود و محاسبه دقیق مقدار شار حرارتی (q) را داریم که در ادامه نحوه محاسبه آن که در هر کوره و صنعت متفاوت است آوردیم.



هنوز کسی نظری نداده! اولین نفر باش...